When light strikes an optical surface some is reflected. How much depends on the refractive index and on the angle of incidence. The fraction reflected, R, is given by the Fresnel equation:
R= [(n1 – n2)/(n1+n2)]2
Where n1 = refractive index of air
( ≃1), n2 = refractive index of the window or lens (n2 ≃1.5 for glass).
The full equation includes angle of incidence but simplifies to this for an angle of 900 (i.e. head-on). For glass, R ≃ 0.04 and so 4% of incident light is reflected, 96% transmitted, at each surface. For a system with 10 optical surfaces (say) the % transmission would be (0.96)10 = 66.5%; a substantial light loss. A camera zoom lens or a pair of binoculars will typically have ~20 optical surfaces and image quality would be further affected by loss in contrast from the scattered light. Anti-reflection (AR) coatings reduce reflection and increase transmission. They work in two ways:
Index-matching
Using a coating with a refractive index between that of glass and air. For example, for a lens coating with n = 1.25, the Fresnel equation tells us that: Rair-coating = 0.0123 and Rcoating-glass = 0.0083. The total reflection is ~2% or about half that of the uncoated surface.
Astute readers might ask, “Then why not keep adding layers with a refractive index between that of the materials on either side?”
In theory it is possible to reduce reflection in this way (see Moth Eye Technology below) using multiple layers such that n increases step-wise from the air to the lens. One limitation is in developing coatings of the required refractive index. E.g. there is no coating with n = 1.25 (which is near the optimum value for a single coating on glass) the closest is probably MgF2 with n = 1.38.
Destructive interference
If light reflected from the lens surface is exactly out of phase with light reflected from a lens coating, the two cancel each other and there is no reflection (assuming equal intensity).
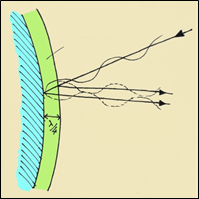The condition for destructive interference is met when the coating thickness is 1/4 of the light wavelength for a specific wavelength at a specific angle of incidence.
In practise, multiple layers are used to address different wavelength regions and give broadband anti-reflection. AR coatings typically reduce reflectivity to ~0.4% over the visible region. Ten optical surfaces, each coated to give 0.4% reflection loss, equates to a total transmission of (0.996)10 = 96.1%; considerably better than the 66.5% transmission with no coating.
A puzzle
How come AR interference coatings increase transmission? Reflected light that is destructively interfering is still reflecting yet it is clear that transmission is considered to have increased (as in the calculation method used in the example shown above).
So, do photons decide not to be reflected if the glass has an interference coating? This seems to be what is happening. Is it another of those things which, deep down, we feel are impossible (like jumbo jets, magnets and …printers) but try not to worry about it too much (in case they’re proof that life is not real perhaps). Or, maybe the explanation includes the word ‘quantum’ (= ‘tbh we don’t really understand it’) and questions our understanding of reality.
The meaning of life etc. will be covered in a later note.
Moth Eye Technology
The ideal non-reflective lens coating would have a continuous refractive index change from 1.0 to 1.5. Moth’s eyes have just this feature and have no reflection losses! This maximises light transmission and removes glare that might otherwise attract predators. Anti-glare screens based on the surface features of moths eyes are being developed for mobile phone screens and could reduce reflection/glare.
Author: Dick Fielding
